The Class 8 is an important year in a student’s life and Maths is one of the subjects that require dedication, hard work, and practice. It’s a subject where you can score well if you are well-versed with the concepts, remember the important formulas and solving methods, and have done an ample amount of practice. Worry not! Home Revise is here to make your Class 8 journey even easier. It’s essential for students to have the right study material and notes to prepare for their board examinations, and through Home Revise, you can cover all the fundamental topics in the subject and the complete NCERT Class 8 Maths Book syllabus.
Find the values of the letters in each of the following and give reasons for the steps involved.
1.
Solution:
Say, A = 7, and we get
7+5 = 12
In which one’s place is 2.
Therefore, A = 7
And putting 2 and carrying over 1, we get
B = 6
Hence, A = 7 and B = 6.
2.
Solution:
If A = 5, we get
8+5 = 13, in which one’s place is 3.
Therefore, A = 5 and carry over 1, then
B = 4 and C = 1
Hence, A = 5, B = 4 and C = 1.
3 .
Solution:
On putting A = 1, 2, 3, 4, 5, 6, 7 and so on, we get
AxA = 6×6 = 36, in which one’s place is 6.
Therefore, A = 6
4.
Solution:
Here, we observe that B = 5, so that 7+5 =12
Putting 2 at one’s place and carrying over 1 and A = 2, we get
2+3+1 =6
Hence, A = 2 and B =5.
5.
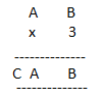
Solution:
Here, on putting B = 0, we get 0x3 = 0.
And A = 5, then 5×3 =15
A = 5 and C = 1
Hence A = 5, B = 0 and C = 1.
6.
Solution:
On putting B = 0, we get 0x5 = 0 and A = 5, then 5×5 =25
A = 5, C = 2
Hence A = 5, B = 0 and C =2
7.
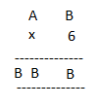
Solution :
Here, products of B and 6 must be the same as one’s place digit is B.
6×1 = 6, 6×2 = 12, 6×3 = 18, 6×4 = 24
On putting B = 4, we get the one’s digit 4, and the remaining two B’s value should be 44.
Therefore, for 6×7 = 42+2 =44
Hence, A = 7 and B = 4.
8.
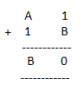
Solution:
On putting B = 9, we get 9+1 = 10
Putting 0 at ones place and carrying over 1, we get A = 7
7+1+1 =9
Hence, A = 7 and B = 9.
9.
Solution:
On putting B = 7, we get 7+1 = 8
Now A = 4, then 4+7 = 11
Putting 1 at tens place and carrying over 1, we get
2+4+1 =7
Hence, A = 4 and B = 7.
10.
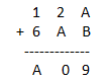
Solution:
Putting A = 8 and B = 1, we get
8+1 = 9
Now, again we add 2 + 8 =10
The tens place digit is ‘0’ and carries over 1. Now 1+6+1 = 8 = A
Hence, A = 8 and B =1.
1. If 21y5 is a multiple of 9, where y is a digit, what is the value of y?
Solution:
Suppose 21y5 is a multiple of 9.
Therefore, according to the divisibility rule of 9, the sum of all the digits should be a multiple of 9.
That is, 2+1+y+5 = 8+y
Therefore, 8+y is a factor of 9.
This is possible when 8+y is any one of these numbers 0, 9, 18, 27, and so on
However, since y is a single-digit number, this sum can be only 9.
Therefore, the value of y should be 1 only, i.e. 8+y = 8+1 = 9.
2. If 31z5 is a multiple of 9, where z is a digit, what is the value of z? You will find that there are two answers to the last problem. Why is this so?
Solution:
Since 31z5 is a multiple of 9,
According to the divisibility rule of 9, the sum of all the digits should be a multiple of 9.
3+1+z+5 = 9+z
Therefore, 9+z is a multiple of 9
This is only possible when 9+z is any one of these numbers: 0, 9, 18, 27, and so on.
This implies, 9+0 = 9 and 9+9 = 18
Hence, 0 and 9 are the two possible answers.
3. If 24x is a multiple of 3, where x is a digit, what is the value of x?
(Since 24x is a multiple of 3, its sum of digits 6+x is a multiple of 3, so 6+x is one of these numbers: 0, 3, 6, 9, 12, 15, 18, … . But since x is a digit, it can only be that 6+x = 6 or 9 or 12 or 15. Therefore, x = 0 or 3 or 6 or 9. Thus, x can have any of four different values.)
Solution:
Let’s say 24x is a multiple of 3.
Then, according to the divisibility rule of 3, the sum of all the digits should be a multiple of 3.
2+4+x = 6+x
So, 6+x is a multiple of 3, and 6+x is one of the numbers: 0, 3, 6, 9, 12, 15, 18 and so on.
Since x is a digit, the value of x will be either 0 or 3 or 6 or 9, and the sum of the digits can be 6 or 9 or 12 or 15, respectively.
Thus, x can have any of the four different values: 0 or 3 or 6 or 9.
4. If 31z5 is a multiple of 3, where z is a digit, what might be the values of z?
Solution:
Since 31z5 is a multiple of 3,
According to the divisibility rule of 3, the sum of all the digits should be a multiple of 3.
That is, 3+1+z+5 = 9+z
Therefore, 9+z is a multiple of 3.
This is possible when the value of 9+z is any of the values: 0, 3, 6, 9, 12, 15, and so on.
At z = 0, 9+z = 9+0 = 9
At z = 3, 9+z = 9+3 = 12
At z = 6, 9+z = 9+6 = 15
At z = 9, 9+z = 9+9 = 18
The value of 9+z can be 9 or 12 or 15 or 18.
Hence 0, 3, 6 or 9 are the four possible answers for z.